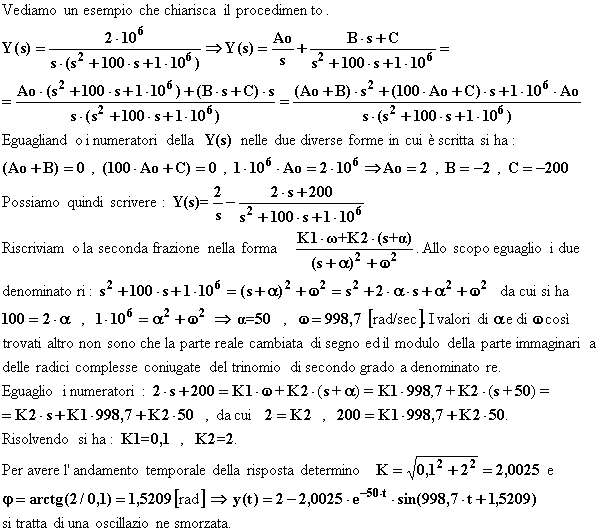Metodi di antitrasformazione

Abbiamo visto che il metodo della trasformata di Laplace richiede, per ottenere infine l'andamento della variabile nel tempo, di antitrasformare la funzione di  s  rappresentante la variabile stessa  nel dominio della frequenza.

 

Se la   Y(s) = N(s) / D(s)   è semplice si utilizza la tabella sotto riportata:

 

 

 

Se la  Y(s)  è complicata, per poter usare la tabella sopra riportata è necessario scomporre la generica frazione rappresentante la  Y(s)  nella somma di più frazioni semplici per ciascuna delle quali sia data l'antitrasformata in tabella. L'antitrasformata della  Y(s)  complessiva si otterrà applicando il principio di linearità di cui gode la trasformata.

 

Il procedimento per la scomposizione della  Y(s)  in una sommatoria di frazioni semplici è diverso a secondo che il denominatore della  Y(s)  si annulli per valori di  s  reali semplici , reali multipli , complessi coniugati.

 

1° caso - Il denominatore di  Y(s) si annulli per valori di  s  tutti reali semplici.

 

In tal caso la  Y(S)  si presenta nella forma:

La somma di frazioni semplici cercata sarà del tipo:

I coefficienti  Ao , A1 , ... , Am (detti residui) si trovano imponendo l'eguaglianza tra il   NUM(s)  ed il numeratore calcolato della somma di frazioni semplici.

 

Esempio:

Si deduce che questo tipo di antitrasformata è pari ad una somma di esponenziali.

2° caso - Il denominatore della  Y(S)  si annulli per valori di s anche reali multipli.

In tal caso a denominatore della Y(s), dopo aver scomposto in fattori, si ha un fattore del tipo

(s - Pi)ⁿ.

 

Vediamo un esempio al fine di dedurre il metodo generale.

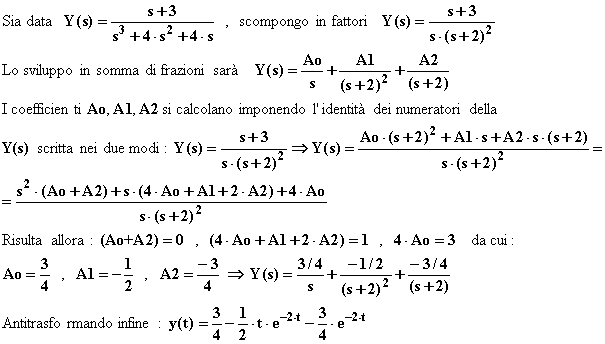
Ancora una volta si ha la somma di termini esponenziali, alcuni dei quali sono però moltiplicati per  t  elevato all'ordine di molteplicità meno uno.

 

3° caso - Il denominatore di  Y(s)  si annulla per valori di  s  anche complessi e coniugati.

Si osserva che la antitrasformata ha i caratteri di una oscillazione di pulsazione w, racchiusa in una fascia delimitata dall'esponenziale di esponente  - a . Ovviamente solo se  - a  è negativo l'oscillazione sarà smorzata. Si verifica che  - a  rappresenta la parte reale delle radici complesse coniugate del trinomio di secondo grado a denominatore mentre  w  ne è la parte immaginaria presa in valore assoluto. Questo tipo di funzioni prende il nome di funzioni cisoidali.

Di particolare interesse è il caso di parte reale negativa, in tal caso l’antitrasformata è un segnale che tende ad un valore finito per il tempo tendente ad infinito. Prende il nome di pulsazione naturale la quantità:

si tratta del modulo del numero complesso.

Viene chiamato coefficiente di smorzamento la quantità:

Per valori del coefficiente di smorzamento inferiori ad uno si hanno delle sovraelongazioni durante il transitorio rispetto al valore assunto a regime tanto più grandi quanto più è piccolo lo smorzamento. Per valori del coefficiente uguali o maggiori di uno la risposta tende asintoticamente al valore finale senza mai superarlo.