La trasformata di Laplace
I sistemi dinamici invarianti e lineari (e tali sono le reti elettriche) possono essere studiati , nel dominio del tempo, attraverso le equazioni differenziali nelle quali l'incognita non è un numero reale, come nelle equazioni algebriche, bensì una funzione del tempo.
Ad esempio la condizione d’equilibrio (legge generalizzata di Ohm) per una rete elettrica costituita dalla serie di un condensatore di capacità C ed una resistenza di valore R, alimentata da un generatore di tensione qualsiasi avente f.e.m. e(t), si scrive:

che costituisce appunto una equazione differenziale dove l’incognita è vc(t), ovvero una funzione del tempo (che oltretutto dipende anche dal valore che nell’istante iniziale aveva la tensione ai capi del condensatore vc(0¯), ovvero che dipende dalle condizioni iniziali). Lo studio analitico di una simile equazione sarà visto nel corso di matematica ove si impareranno le regole per la risoluzione delle equazioni differenziali.
Lo studio dei transitori, tuttavia, diventa più agevole, pur restando rigoroso, se si trasferisce il calcolo dal campo reale, ove le variabili sono funzione del tempo t , al campo complesso, ove le variabili sono funzione di s = s + j w ed s è chiamata frequenza complessa.
Tale operazione avviene mediante la trasformazione di Laplace:
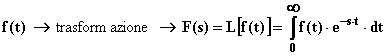
dove deve essere f(t)=0 per t<0 , f(t) definita per ogni t ³ 0 , f(t) soddisfacente alle condizioni di Dirichlet in ogni intervallo finito di tempo (ovvero presentare un numero finito di discontinuità, oscillare tra un valore massimo e minimo un numero finito di volte, assumere solamente valori finiti). Tali condizioni sono, almeno nelle applicazioni che ci interessano, sempre soddisfatte.
E' possibile anche la antitrasformazione ossia il passaggio dalla F(s) alla f(t):
![]()
Esiste quindi una corrispondenza biunivoca tra le funzioni f(t) trasformabili secondo Laplace e le loro trasformate F(s). Nei casi più comuni non è necessario calcolare l'integrale ma è sufficiente consultare la tabella riportata nelle pagine seguenti.
Le regole fondamentali di trasformazione, utilizzate nelle applicazioni che ci interessano, sono le seguenti:
1) La trasformata di Laplace del prodotto di una costante K per la funzione f(t) è data dal prodotto fra la costante stessa e la trasformata F(s) della f(t):
L[ K·f(t) ] = K·F(s)
2) La trasformata della derivata di una funzione f(t) è data dalla trasformata F(s) della funzione moltiplicata per s e diminuita del valore f(0-) che la funzione assume all'istante t = 0- (condizioni iniziali); in detto enunciato è anche riassunto il cosiddetto teorema della trasformata della derivata generalizzata:
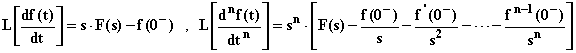
3) La trasformata dell'integrale di una funzione f(t) corrisponde alla F(s) divisa per s:
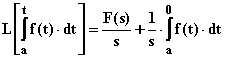
dove, nei casi pratici, l’integrale scritto a secondo membro altro non è che la grandezza f(t)·t calcolata nell’istante iniziale.
4) Teorema del valore iniziale: il valore assunto dalla funzione f(t) all'istante t=0 si ottiene moltiplicando s per la trasformata della funzione stessa e calcolandone successivamente il limite per s tendente all'infinito:
![]()
5) Teorema del valore finale: il valore assunto dalla funzione f(t) quando t tende a infinito si ottiene moltiplicando s per la trasformata della funzione stessa e calcolandone successivamente il limite per s che tende a 0. Questo teorema vale solo se il denominatore della s·F(s) ha radici tutte a parte reale minore di zero.
![]()
Questi due teoremi consentono di valutare rispettivamente il valore iniziale e quello finale (condizione di regime statico) della grandezza assoggettata ad un fenomeno transitorio, nota che sia la trasformata della grandezza stessa.
6) La trasformata della somma di due funzioni f1(t) e f2(t) è data dalla somma delle trasformate delle due funzioni (la stessa regola vale anche per le antitrasformate):
L [ f1(t) + f2(t) ] = F1(s) + F2(s)
7) Teorema della moltiplicazione per t:
![]()
8) Teorema della traslazione in s:
![]()
Ovvero una traslazione a nel dominio della variabile s corrisponde nel tempo a moltiplicare per la quantità e-a·t .
9) Teorema della traslazione nel tempo:
![]()
Ovvero una traslazione t nel dominio del tempo corrisponde a moltiplicare per il termine e-s·t nel dominio della s.
Il grande vantaggio di condurre l'analisi del transitorio nel dominio della frequenza complessa consiste nel fatto che la trasformazione di Laplace consente di ricondurre operazioni con derivate ed integrali ad operazioni algebriche ovvero di ricondurre equazioni differenziali ad equazioni algebriche. Quindi, in linea del tutto generale, possiamo concludere che assegnata una qualsiasi equazione differenziale, purché siano rispettate le condizioni sopra richiamate, è possibile mediante la trasformata di Laplace passare dal dominio del tempo al dominio della frequenza complessa, risolvere algebricamente l’equazione in s così ottenuta, ed infine antitrasformare per avere la soluzione nel dominio del tempo.