Esempio 3, rete RLC sollecitata in corrente continua

 

Assegnata la rete elettrica di figura, determinare in funzione del tempo la legge di variazione delle correnti che circolano nell'induttore e nel condensatore quando, all'istante considerato come iniziale, si chiude il tasto  T:

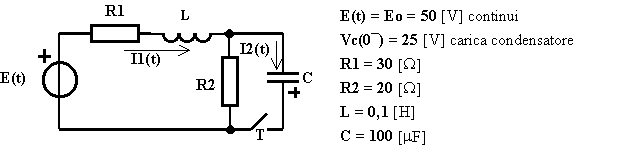
Alla chiusura del tasto  T  la rete può essere trasformata in quella topologicamente equivalente sotto riportata, nella quale si è tenuto conto delle condizioni iniziali non di quiete a causa della corrente circolante nell'induttore e della carica del condensatore presenti ancor prima di chiudere il tasto  T:

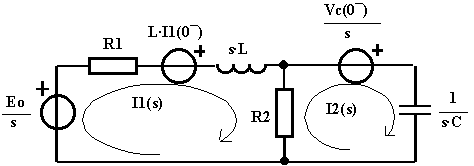
Determino per prima cosa il valore della forza elettromotrice dei due generatori di tensione fittizi che tengono conto delle condizioni iniziali non nulle:

Applicando il metodo di Maxwell, dopo aver fissato il verso delle correnti di maglia, si può scrivere:

 

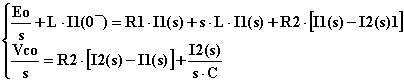
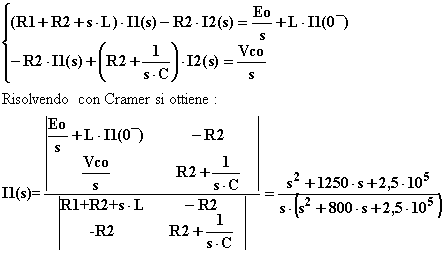
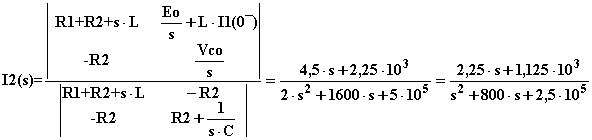
Dopo aver determinato le grandezze richieste nel dominio della frequenza complessa, per conoscerne l'andamento nel dominio del tempo si rende necessaria la loro antitrasformazione. Entrambi i denominatori presentano radici complesse coniugate, quindi entrambe le variabili conterranno termini cisoidali.

 

Antitrasformo I2(s):

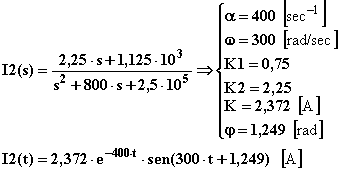
Antitrasformo  I1(s):

 

 

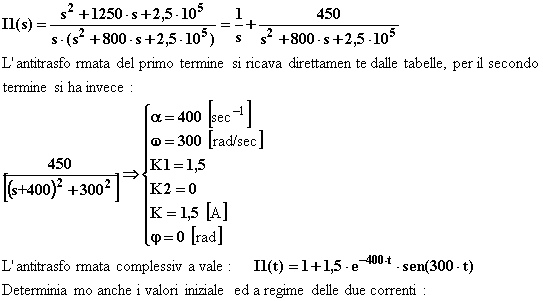
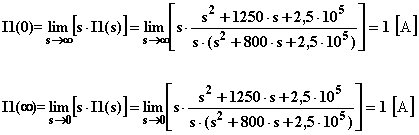
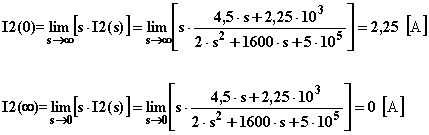
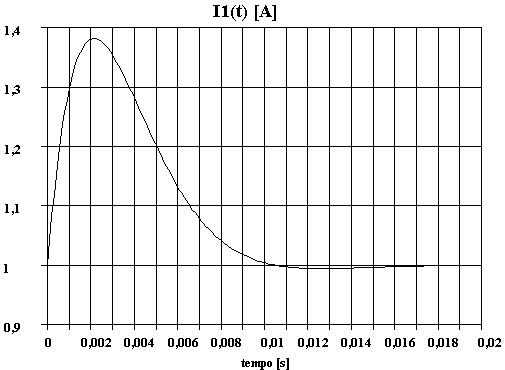
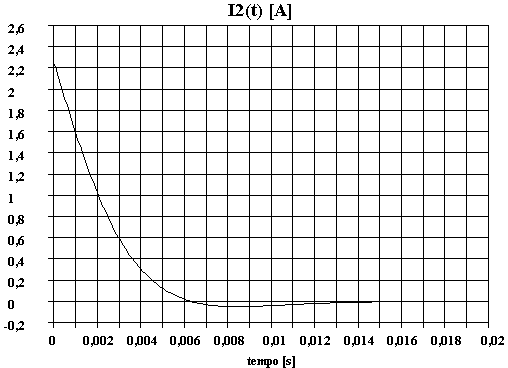
Vediamo l’andamento grafico delle due correnti durante l’evolversi del transitorio: