Analisi del transitorio mediante la funzione di trasferimento

 

Presa una qualsiasi rete elettrica, comunque complessa, inizialmente in quiete (nessuna carica sulle armature dei condensatori e nessuna corrente attraverso gli induttori nell'istante  t = 0¯ [sec]) nella quale agisca un solo bipolo attivo, assunta  X(t)  quale grandezza di ingresso ed  Y(t)  quale grandezza d'uscita (X(t)  ed  Y(t)  possono indifferentemente essere tensioni o correnti) viene definita funzione di trasferimento  H(s):

 

 

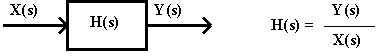
dove X(s) è la trasformata dell'ingresso X(t)  ed  Y(s)  è la trasformata dell'uscita  Y(t).

 

Tale linguaggio è mutuato direttamente da quello tipico dei Controlli Automatici per lo studio dei quali la funzione di trasferimento costituisce uno strumento importantissimo.

 

La funzione di trasferimento non dipende dalla particolare funzione del tempo in ingresso, ma solo dai parametri caratteristici della rete ed è, quindi, tipica per ciascuna rete.

L'uscita di una rete nel dominio complesso è data dal prodotto della trasformata dell'ingresso per la funzione di trasferimento. Quindi, se l'ingresso è la funzione impulsiva, avendo questa trasformata pari ad 1, si potrà affermare che l'uscita si identifica con la funzione di trasferimento. Da questo caso particolare si può ricavare un'altra interpretazione della funzione di trasferimento di una rete: essa coincide con la trasformata di Laplace della risposta della rete ad un impulso unitario in ingresso (purché le condizioni iniziali siano nulle e l'unico bipolo attivo sia quello che determina l'impulso).

Per il calcolo della funzione di trasferimento di una rete è conveniente prendere in considerazione la rete equivalente nel dominio della frequenza complessa ed applicare ad essa i metodi tradizionali di analisi delle reti lineari.

 

Il procedimento che permette di individuare la variazione dell'uscita di una rete elettrica conseguente alla applicazione di un segnale al suo ingresso si sviluppa attraverso i seguenti passi:

 

1)   si determina la funzione di trasferimento  H(s)  della rete elettrica;

2)   si   trasforma  il segnale di ingresso   X(t)  nel corrispondente   X(s)  consultando l'apposita tabella;

3)   si calcola la trasformata dell'uscita  Y(s) = X(s)·H(s);

4)  si antitrasforma  Y(s)  in  Y(t)  ottenendo così la legge con cui l'uscita si evolve nel tempo.

Osservazione: la trattazione della funzione di trasferimento fatta in questo momento è assolutamente riduttiva rispetto quanto è necessario conoscere sul tale argomento nell'ambito della disciplina dei Controlli Automatici. In effetti noi vediamo (al momento) la funzione di trasferimento soltanto quale strumento per la determinazione del transitorio in una rete elettrica, trascurando totalmente le implicazioni riguardo alla stabilità ed alla risposta in frequenza della rete.