Esempio 6, rete RLC sollecitata con diversi segnali
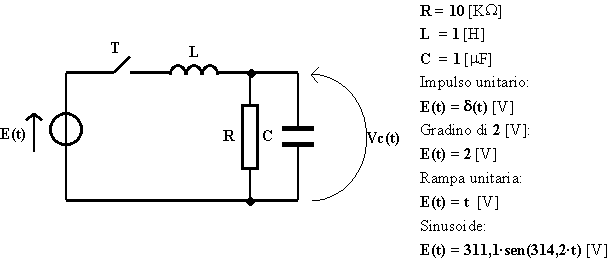
Assegnata la rete elettrica di figura, assumendo che essa sia inizialmente a riposo, determinare l'andamento della tensione Vc(t) ai capi del condensatore a partire dall'istante di chiusura dell'interruttore T per i vari tipi di ingresso indicati:
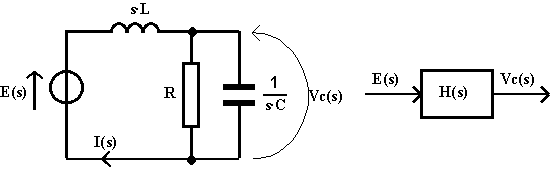
Per prima cosa disegno la rete topologicamente equivalente alla data ma con le grandezze formulate nel dominio della frequenza complessa:
Determino quindi la funzione di trasferimento. Allo scopo applico le tecniche di analisi tipiche per le reti lineari:
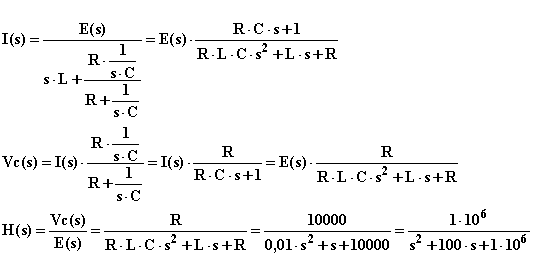
La trasformata del segnale di ingresso del tipo impulsivo vale:
![]()
La trasformata del segnale di ingresso del tipo a gradino vale:
![]()
La trasformata del segnale di ingresso del tipo a rampa vale:
![]()
La trasformata del segnale di ingresso del tipo sinusoidale vale:
![]()
La trasformata dell'uscita, il valore iniziale ed il valore a regime quando in ingresso vi è un impulso unitario valgono:
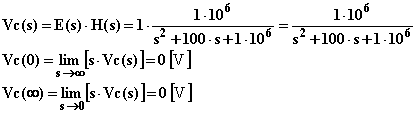
La trasformata dell'uscita, il valore iniziale ed il valore a regime quando in ingresso vi è un gradino valgono:
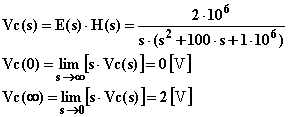
La trasformata dell'uscita, il valore iniziale ed il valore a regime quando in ingresso vi è una rampa valgono:
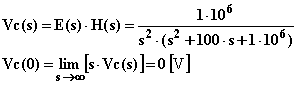
Il teorema del valore finale non è applicabile in quanto la funzione s·Vc(s) presenta a denominatore una radice nulla. In effetti Vc(t) per t tendente ad infinito tende pure ad infinito.
La trasformata dell'uscita, il valore iniziale ed il valore a regime quando in ingresso vi è una sinusoide valgono:
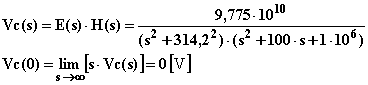
Il teorema del valore finale non è applicabile in quanto la funzione s·Vc(s) presenta a denominatore una coppia di radici immaginarie e quindi a parte reale nulla. In effetti a regime l'uscita sarà una grandezza sinusoidale e quindi sarà contenuta fra un valor massimo ed un valor minimo, oscillando tra detti valori.
L'uscita nel dominio del tempo quando in ingresso vi è un impulso unitario si determina antitrasformando la associata Vc(s):
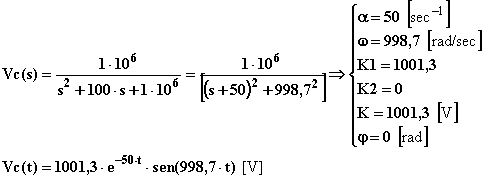
Si tratta di una funzione cisoidale e più precisamente di una oscillazione esponenziale smorzata il cui andamento è il seguente:
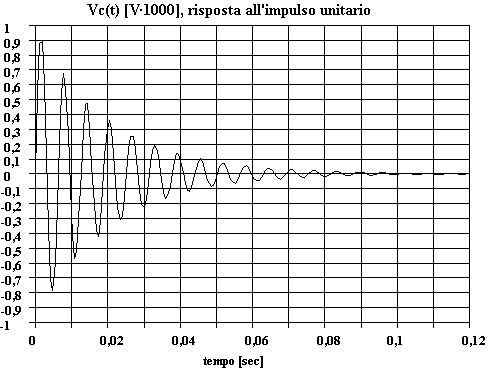
L'uscita nel dominio del tempo quando in ingresso vi è un gradino di 2 [V] si determina antitrasformando la associata Vc(s), cosa già fatta nel paragrafo relativo ai metodi di antitrasformazione:
![]()
Si tratta di un termine costante cui si sovrappone una funzione cisoidale costituita da una oscillazione esponenziale smorzata; l'andamento complessivo è il seguente:
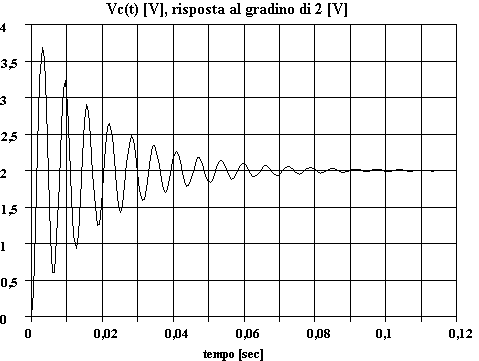
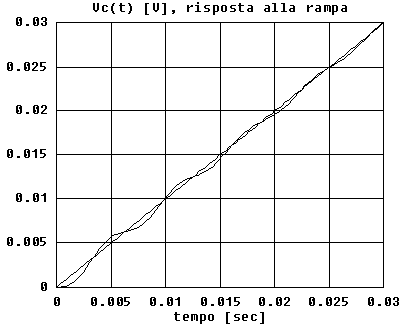
L'uscita nel dominio del tempo quando in ingresso vi è una rampa unitaria si determina antitrasformando la associata Vc(s):
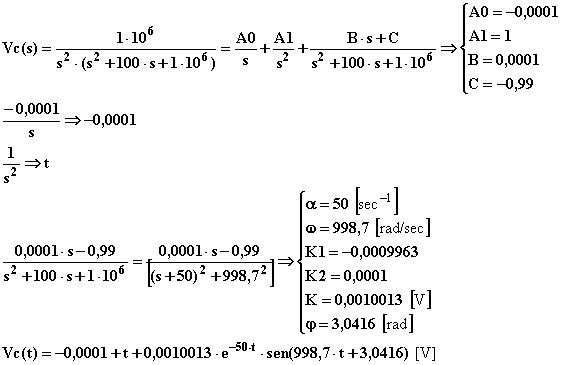
L'oscillogramma corrispondente è il seguente:
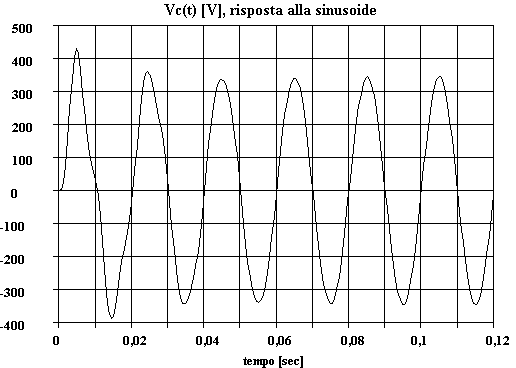
L'uscita nel dominio del tempo quando in ingresso vi è una sinusoide si determina antitrasformando la associata Vc(s):
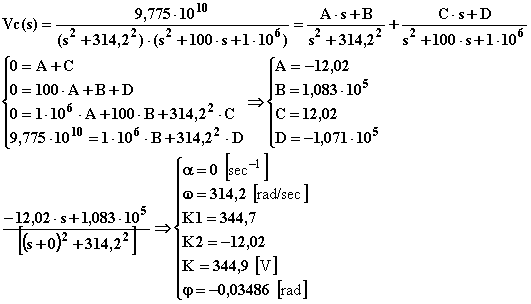
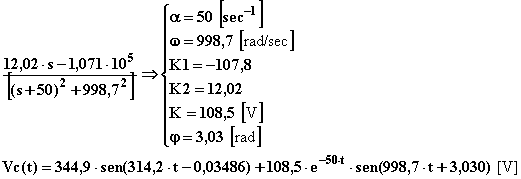
Il primo termine corrisponde alla sinusoide di regime raggiunto, il secondo alla parte transitoria che si esaurirà dopo un tempo pari a circa cinque volte la costante di tempo ovvero (5·1/50)=0,1 [sec]. L'oscillogramma è il seguente: