Esempio 1, rete RL sollecitata da un generatore di tensione continua

 

Data la rete di figura nella quale Vo=24 [V], R=10 [W], L=0,5 [H], determinare come varia nel tempo l’intensità della corrente a partire dall’istante di chiusura dell’interruttore.

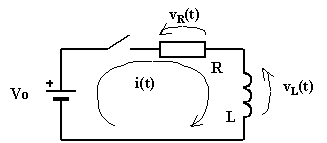
Per prima cosa scrivo l’equazione che rappresenta l’equilibrio elettrico della rete (legge di Ohm generalizzata):

dove:

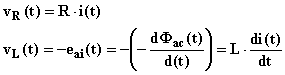
Sostituendo si ha infine:

Si tratta di una equazione differenziale avente per incognita i(t). Per la sua risoluzione è necessario conoscere le condizioni iniziali, ovvero il valore che aveva la grandezza incognita immediatamente prima dell’istante iniziale. Risulta del tutto evidente che tale condizione non può essere che i(0^-)=0 [A].

Risolviamo tale equazione mediante la trasformata di Laplace.

Per prima cosa trasformo tutti i termini dell’equazione:

Utilizzando la tabella e le proprietà della trasformata si ottiene:

Questa è un’equazione algebrica che risolvo rispetto I(s):

Si osservi come l’espressione finale sia stata scritta mettendo in evidenza a denominatore tutti i fattori, ciascuno con il termine in s di grado maggiore col coefficiente unitario. E’ questa una forma conveniente in quanto le tabelle di trasformazione presentano le espressioni in s proprio nella stessa forma.

Ora bisogna antitrasformare I(s) per avere i(t). L’espressione ottenuta non è una frazione semplice presente in tabella e per tale motivo bisogna provvedere alla sua rielaborazione. Siamo nel caso di radici a denominatore tutte reali e semplici, quindi si procede nel seguente modo:

Perché le due espressioni di I(s) corrispondano dovrà essere:

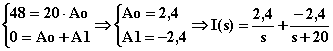
Adesso è possibile applicare a ciascun termine della I(s) la tabella di antitrasformazione:

 [A]

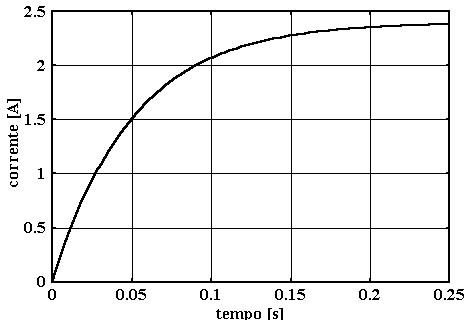
Questa è la soluzione del problema proposto. Si tratta di una esponenziale crescente avente costante di tempo pari a 1/20= 0,05 [s], ovvero pari a L/R come già sapevamo dalla Elettrotecnica. A regime raggiunto la corrente varrà i(¥)=2,4 [A], anche questo concorda con quanto già noto dall’Elettrotecnica, infatti in una rete in corrente continua, a regime, l’induttanza si comporta come un cortocircuito così che la corrente risulta limitata dalla sola resistenza. Nell’istante iniziale i(0)=0 [A], infatti la presenza dell’induttanza impedisce alla corrente di avere una variazione finita in un tempo infinitesimo in modo tale che la corrente all’istante iniziale deve essere uguale a quella che si aveva prima della chiusura dell’interruttore.

 

L’aspetto del grafico della i(t) è il seguente: