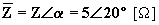Esercizio N° 1 (sistema a tre fili simmetrico, carico equilibrato a stella, caso di guasto )

 E’ dato un sistema trifase a tre fili, simmetrico nelle tensioni, V = 380 [V], f = 50 [Hz], che alimenta tre impedenze uguali di valore 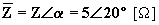collegate a stella.

Determinare :

a) le tensioni applicate a ciascuna impedenza, le correnti di linea, le potenze attiva e reattiva complessive, le indicazioni di due wattmetri inseriti secondo Aron sui fili di linea 3 e 1;

b) ipotizzando che a causa di un guasto l’impedenza collegata alla fase 2 si interrompa, rideterminare le tensioni applicate alle singole impedenze, le correnti di linea, le potenze attiva e reattiva complessive, le indicazioni di tre wattmetri inseriti secondo Righi;

c) ipotizzando che a causa di un guasto l’impedenza collegata alla fase 2 vada in cortocircuito, rideterminare le tensioni applicate alle singole impedenze, le correnti di linea, le potenze attiva e reattiva complessive, le indicazioni di quattro wattmetri inseriti secondo Barbagelata.

Risoluzione

 Risposta alla domanda a)

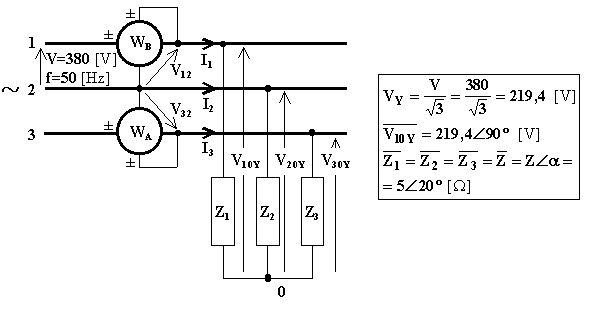
Essendo il carico a stella ed equilibrato, su ciascuna impedenza è applicata la corrispondente tensione stellata del sistema simmetrico di tensioni trifasi e, quindi,:

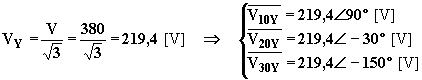
Le correnti di linea, essendo il carico equilibrato, costituiranno una terna simmetrica di vettori sfasata dell’angolo j = a = 20° rispetto alla terna di tensioni stellate (inoltre, essendo le impedenze di natura ohmico-induttiva perché a > 0°, le correnti saranno in ritardo sulle tensioni stellate). L’intensità delle tre correnti è la stessa e i valori simbolici delle correnti di linea sono:

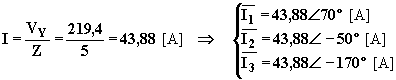
Le potenze attiva e reattiva complessive, essendo il sistema simmetrico ed equilibrato, si possono determinare con le espressioni:

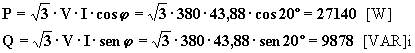
 Le indicazioni di due wattmetri inseriti secondo Aron sui fili 3 e 1 valgono rispettivamente:

 Si può immediatamente verificare che, a meno della cifra approssimata, è:

 Il diagramma vettoriale sul piano di Gauss rappresentante le tensioni e correnti calcolate è il seguente:

 Risposta alla domanda b)

Se l’impedenza Z2 si interrompe, il carico trifase si squilibra così che il centro stella 0’ viene ad assumere un potenziale diverso da quello che competerebbe al filo neutro se fosse presente. Il sistema si può studiare ricorrendo allo spostamento del centro stella, oppure applicando semplicemente la legge di Ohm. Vediamo il secondo metodo, per quanto riguarda le correnti si ha:

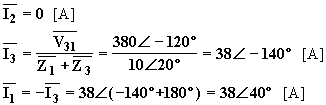
 Per le tensioni si ha:

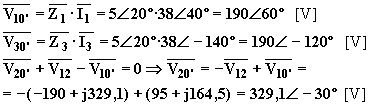
 Lo spostamento del centro stella vale:

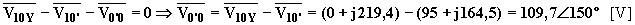
 Le potenze attiva e reattiva si dovranno calcolare applicando il teorema di Boucherot:

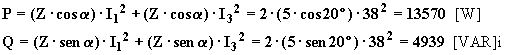
 Le indicazioni dei tre wattmetri inseriti secondo Righi saranno le seguenti:

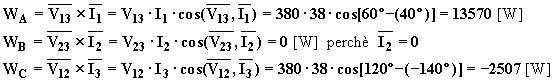
 Si può immediatamente verificare che, a meno della cifra approssimata, è:

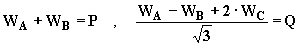
Il diagramma vettoriale sul piano di Gauss rappresentante le tensioni e correnti calcolate è il seguente:

 

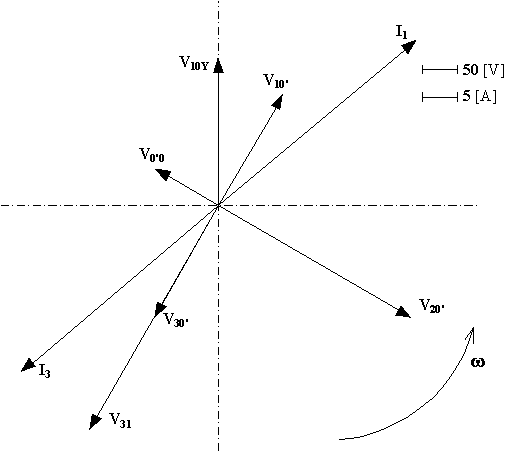
Risposta alla domanda c)

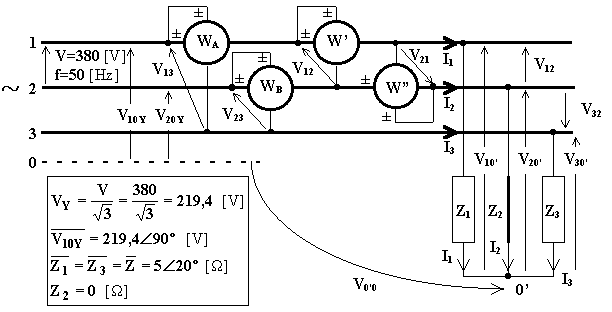
Se l’impedenza Z2 si cortocircuita, il carico trifase si squilibra così che il centro stella 0’ viene ad assumere un potenziale diverso da quello che competerebbe al filo neutro se fosse presente. Più precisamente il centro stella 0' coincide col punto 2 e lo spostamento del centro stella vale la tensione stellata V20Y. Il sistema si può studiare applicando semplicemente la legge di Ohm. Per quanto riguarda le correnti si ha:

 Per le tensioni applicate alle singole impedenze si ha:

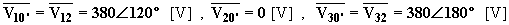
 Lo spostamento del centro stella vale:

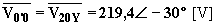
 Le potenze attiva e reattiva si dovranno calcolare applicando il teorema di Boucherot:

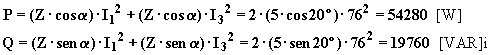
 Le indicazioni dei quattro wattmetri inseriti secondo Barbagelata saranno le seguenti:

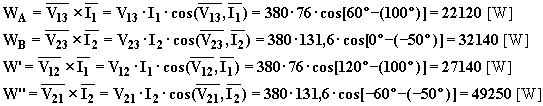
 Si può immediatamente verificare che, a meno della cifra approssimata, è:

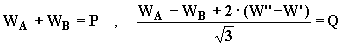
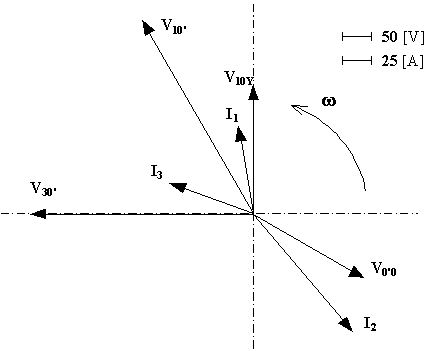
Il diagramma vettoriale sul piano di Gauss rappresentante le tensioni e correnti calcolate è il seguente:

Sistemi trifasi
Programma per la classe quarta
Home Page