Esercizio 1 (campo magnetico in un solenoide, induttanza,
f.e.m. autoindotta, energia)
Si abbia un solenoide rettilineo lungo l = 100 [cm] di sezione circolare formato da N = 1500 spire di diametro d = 8 [cm] disposte in un unico strato e strettamente affiancate tra di loro. Il solenoide sia avvolto in aria e sia percorso dalla corrente continua I = 5 [A]:

1) determinare il campo magnetico, l’induzione ed il flusso all’interno del solenoide.
Nei solenoidi rettilinei lunghi (ovvero di lunghezza almeno dieci volte maggiore del diametro) ed avvolti a spire serrate con verso omogeneo, il campo magnetico all’interno è praticamente uniforme e di intensità pari a:
![]()
Le linee di campo magnetico all’interno sono parallele all’asse del solenoide ed hanno verso determinato dal senso di avvolgimento e dal verso della corrente. Con riferimento alla figura, applicando la regola della vite ed immaginando quindi di ruotare la vite secondo il verso col quale la corrente percorre l’avvolgimento avremo che la vite avanzerà verso destra, quindi questo è il verso del campo all’interno del solenoide. Un altro modo per individuare il verso del campo consiste nell’immaginare di prendere nel palmo della mano il solenoide in modo tale che la corrente percorra la parte di avvolgimento a contatto con la mano con verso che va dal polso alle dita: il pollice indicherà il verso del campo.
L’induzione magnetica si determina moltiplicando il campo per la permeabilità magnetica del mezzo nel quale il campo si sviluppa. Nel nostro caso essendo il mezzo l’aria assumeremo come valore della permeabilità quello del vuoto:
![]()
Il flusso di induzione magnetica si determina moltiplicando l’induzione per la sezione interna del solenoide calcolata trasversalmente alle linee di campo:
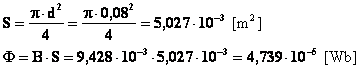
Sia l’induzione che il flusso hanno sempre lo stesso verso del campo.
2) calcolare l’induttanza del solenoide.
L’induttanza (detta anche coefficiente di autoinduzione) di un qualsiasi circuito elettrico è per definizione il rapporto tra il flusso autoconcatenato col circuito e l’intensità della corrente che circolando nel circuito stesso produce il flusso.
In un solenoide il flusso autoconcatenato si calcola moltiplicando il flusso prodotto dalla corrente circolante nell’avvolgimento per il numero di spire che compone l’avvolgimento (naturalmente tutte le spire devono essere avvolte nello stesso senso). Infatti il flusso si concatena col circuito ogniqualvolta interseca il piano delimitato da una spira. Nel nostro caso:
![]()
L’induttanza vale quindi:
![]()
Osservazione: i dispositivi che come il solenoide hanno lo scopo di realizzare un valore concentrato di induttanza sono chiamati induttori. E’ importante non confondere gli induttori con i reostati a filo avvolto. Infatti questi ultimi hanno lo scopo di realizzare un valore concentrato di resistenza e per questo scopo il conduttore che si impiega non è il rame bensì una lega resistiva (manganina, costantana, ferro-nichel. ecc.). Inoltre il filo conduttore di lega resistiva viene avvolto sul supporto in un numero pari di strati invertendo il verso di avvolgimento passando da strato a strato al fine di rendere il più piccolo possibile il flusso autoconcatenato e l’induttanza (che in questo dispositivo è un parametro elettrico parassita).
3) determinare l’energia immagazzinata nel campo magnetico interno al solenoide.
Questa energia si può calcolare attraverso l’espressione:
![]()
Oppure si può calcolare attraverso l’energia specifica interna al campo magnetico:
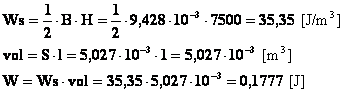
4) supponendo che l’intensità della corrente si annulli nel tempo di un centesimo di secondo, calcolare il valore medio della forza elettromotrice autoindotta Eai che si sviluppa in tale intervallo di tempo nel solenoide.
Per la legge generale dell’induzione elettromagnetica, la variazione di corrente nel solenoide comporta la variazione di flusso autoconcatenato e quindi lo sviluppo di una forza elettromotrice chiamata autoindotta in quanto prodotta dalla variazione del flusso dovuto alla stessa corrente presente nel circuito.
Per prima cosa individuiamo il verso di tale f.e.m. autoindotta. A tale scopo bisogna tenere presente che essa deve opporsi alla causa che l’ha generata. Siccome la causa è una diminuzione della corrente e quindi del flusso autoconcatenato, per opporsi a tale diminuzione la f.e.m. autoindotta dovrà essere tale da sostenere la corrente e quindi si presenterà ai morsetti del solenoide con le polarità di figura:
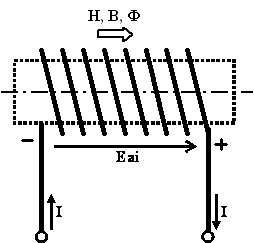
Ovviamente se, a differenza del caso in esame, la corrente variasse aumentando, il verso della f.e.m. autoindotta sarebbe opposto a quello appena determinato in quanto comunque la f.e.m. deve opporsi alla causa che l’ha generata.
La sua intensità si calcola applicando la legge generale dell’induzione elettromagnetica:
![]()
la variazione di flusso autoconcatenato è stata calcolata facendo il flusso finale (zero perché se si annulla la corrente si annulla anche il flusso) meno il flusso iniziale.
Lo stesso risultato, ricordando la definizione di induttanza, si ottiene anche nel seguente modo:
![]()
Osservazione: da quanto fino ad ora esposto risulta evidente il diverso comportamento elettrico dell’induttanza nel caso in cui la corrente che l’attraversa vari nel tempo rispetto al caso in cui rimanga costante. Se la corrente varia nel tempo l’induttanza reagisce opponendosi a tale variazione attraverso lo sviluppo della f.e.m. autoindotta, se invece la corrente è costante l’induttanza non produce alcun effetto comportandosi come se fosse un cortocircuito.
Campi e circuiti magnetici
Programma per la classe terza
Home Page