Esercizio 3 (circuito magnetico tutto serie, problema diretto)

Si abbia il seguente circuito magnetico:

Il circuito magnetico sia composto da due tronchi in materiale ferromagnetico e da un traferro.

Le dimensioni geometriche siano l₁=30 [cm], S₁=12 [cm²] per il tronco in ghisa, l₂=10 [cm], S₂= 8 [cm²] per il tronco in lamierini normali (la lunghezza è quella della linea di induzione media misurata come indicato nella figura e la sezione è quella netta trasversale alla linea di induzione media). Il traferro abbia estensione l_T=1,5 [mm] e la sua sezione sia del 5% maggiore di S₁ a causa dell’effetto ai bordi delle linee di campo magnetico (si tratta del fenomeno della espansione laterale delle linee di forza).

Sul circuito magnetico agiscano due avvolgimenti, il primo composto da N₁=100 spire e percorso dalla corrente I₁= 40 [A] col verso di figura, il secondo composto da N₂=75 spire. Infine si trascurino eventuali flussi dispersi.

1) determinare l’intensità che deve avere la corrente I₂ nel secondo avvolgimento affinché il campo magnetico nel traferro valga H_T= 800000 [A/m] ed abbia il verso dall’alto al basso.

Il tipo di problema proposto è sicuramente del tipo diretto in quanto è fornito il campo magnetico in un tratto del circuito così che diventa possibile trovare direttamente l’induzione ed il campo in ogni altro tratto e applicare la legge della circuitazione magnetica (metodo delle forze magnetomotrici parziali) o la legge di Hopkinson (metodo delle riluttanze) al fine di determinare la corrente incognita.

Noi risolviamo col metodo delle forze magnetomotrici parziali. Per prima cosa bisogna assegnare un verso arbitrario alla corrente incognita I₂ nel secondo avvolgimento, nel nostro caso scegliamo il verso di figura.

Quindi andiamo a determinare per ogni tronco omogeneo (si intende un tratto di circuito caratterizzato da uniformità di materiale, di sezione e di flusso) del circuito il campo magnetico e la lunghezza.

Traferro:

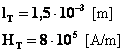
Tronco in ghisa:

Per trovare il campo considero che essendo il circuito tutto serie il flusso sarà lo stesso in tutti i tronchi. Avendo poi imposto il campo nel traferro diretto dall’alto al basso, il flusso circolerà nel circuito con verso orario. Il valore del flusso varrà:

L’induzione nella ghisa varrà:

Per conoscere il campo magnetico nella ghisa dovrò consultare le caratteristiche di magnetizzazione di questo materiale. Tali caratteristiche riportano:

Eseguendo una interpolazione lineare tra le due coppie ho:

Tronco in lamierini normali:

Per conoscere il campo magnetico nelle lamiere dovrò consultare le caratteristiche di magnetizzazione di questo materiale. Tali caratteristiche riportano:

Eseguendo una interpolazione lineare tra le due coppie ho:

Ora che ho il campo e la lunghezza per ciascun tronco posso applicare la legge della circuitazione magnetica.

Questa legge dice che lungo una linea chiusa la somma aritmetica delle cadute di tensione magnetica eguaglia la somma algebrica delle forze magnetomotrici (le forze magnetomotrici si prendono positive se agiscono concordemente col verso della linea chiusa assunto positivo). Si sceglie come linea chiusa la linea di induzione media e come verso positivo il verso del flusso.

Con tali presupposti è facile verificare che la forza magnetomotrice del primo avvolgimento è da prendersi positiva mentre la forza magnetomotrice del secondo avvolgimento è da prendersi negativa. L’equazione rappresentante la legge della circuitazione diventa quindi:

Risolvendo rispetto I₂ si ha infine:

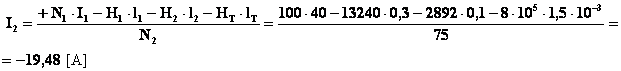
Il fatto che la corrente da determinarsi sia risultata negativa significa che al fine di ottenere nel traferro il campo desiderato bisogna imporre nel secondo avvolgimento una corrente di 19,48 [A] con verso opposto a quello prefissato, ovvero anche il secondo avvolgimento deve produrre una forza magnetomotrice concorde col verso del flusso.

2) Determinare la tensione magnetica ai capi del tronco in ghisa.

La tensione magnetica tra i punti D e A può essere trovata in due diversi modi, in ogni caso si applica al circuito magnetico l’analogo della legge di Ohm applicata ad un tratto di circuito elettrico.

Se uso il tratto comprendente il tronco in ghisa e l’avvolgimento fatto di N₁ spire ho:

Se uso il tratto comprendente il traferro ed il tronco in lamiere con l’avvolgimento fatto di N₂ spire ho:

.

3) Risolvere lo stesso circuito usando il metodo delle riluttanze.

Per prima cosa si disegna il circuito magnetico in forma analoga ad un circuito elettrico:

Quindi si determinano le riluttanze che compongono il circuito.

Riluttanza del traferro:

Riluttanza del tronco in ghisa:

Per conoscere la permeabilità magnetica relativa nella ghisa dovrò consultare le caratteristiche di magnetizzazione di questo materiale. Tali caratteristiche riportano:

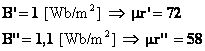
Eseguendo una interpolazione lineare tra le due coppie ho:

Riluttanza del tronco in lamierini normali:

Per conoscere la permeabilità magnetica relativa nelle lamiere dovrò consultare le caratteristiche di magnetizzazione di questo materiale. Tali caratteristiche riportano:

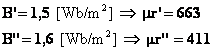
Eseguendo una interpolazione lineare tra le due coppie ho:

Note le riluttanze, applico la legge di Hopkinson al circuito magnetico (in modo analogo alla legge do Ohm applicata ad un circuito elettrico chiuso, con la forza magnetomotrice che corrisponde alla forza elettromotrice, il flusso che corrisponde alla corrente e la riluttanza che corrisponde alla resistenza):

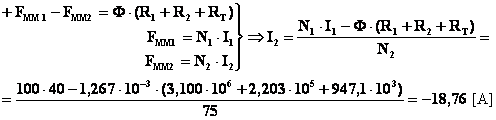
Osservazione: la differenza numerica tra le due soluzioni dipende dal fatto che si sono utilizzati i valori tabulati di campo e di permeabilità relativa che sono stati rilevati sperimentalmente e dal fatto che è stato necessario effettuare su tali valori delle interpolazioni lineari (essendo le caratteristiche di magnetizzazione e di permeabilità diverse tra di loro, l’interpolazione lineare introduce nei due casi errori diversi). Per gli stessi motivi, le cadute di tensione magnetica danno risultati leggermente diversi a seconda che siano calcolate come (H·l) oppure come (Φ·R).

Campi e circuiti magnetici
Programma per la classe terza
Home Page

---