Esercizio 4 (circuito magnetico tutto serie, problema inverso)
Si abbia un circuito magnetico di ghisa di forma toroidale avente un traferro dallo spessore costante pari a lT=3 [mm]. La lunghezza della circonferenza media, compreso il traferro, è lm=60 [cm] e la sezione del nucleo di ghisa è S1=16 [cm2]. L’avvolgimento di eccitazione è disposto uniformemente sulla metà del nucleo opposta al traferro ed è composto di N=600 spire percorse dalla corrente I=2 [A]. Si trascurino gli eventuali flussi dispersi e si consideri la sezione del traferro maggiorata del 5% rispetto alla sezione del nucleo in ghisa a causa dell’effetto ai bordi delle linee di campo magnetico.

1) Determinare il flusso presente nel circuito magnetico.
Essendo il circuito magnetico tutto serie, il flusso avrà lo stesso valore in tutte le sezioni. Il verso del flusso si determina immediatamente conoscendo il senso di avvolgimento delle spire ed il verso della corrente nell’avvolgimento. Nel caso in esame il verso del flusso sarà quello orario.
La determinazione del valore del flusso è invece molto più problematica. Infatti si conosce la forza magnetomotrice assegnata che vale:
![]()
ma, essendo il circuito composto di più tronchi (due nel
nostro caso, il nucleo in ghisa ed il traferro) accade che la non linearità
della caratteristica di magnetizzazione rende impossibile determinare il valore
della permeabilità o del campo magnetico nelle diverse parti del circuito
mediante l'applicazione diretta di equazioni risolutrici. Bisogna quindi
procedere per tentativi applicando il seguente algoritmo:

passo a)
Scegliamo per l’accuratezza della risoluzione un valore pari al 5% (è inutile scegliere un valore migliore in quanto le tabelle di magnetizzazione delle quali disponiamo sono piuttosto grossolane). Quindi riterremo accettabile la soluzione per la quale la forza magnetomotrice necessaria a sostenere il flusso calcolato sarà compresa nella fascia di valori:
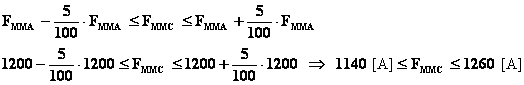
passo b)
Scegliamo pari a B1= 0,6 [Wb/m2] il valore dell’induzione nel tronco in ghisa per il primo tentativo. Questo valore è stato fissato considerando che è centrale nella tabella di magnetizzazione della ghisa a nostra disposizione ove i valori possibili variano tra 0,1 ed 1,2 [Wb/m2].
passo c)
Calcoliamo la FMMC necessaria a sostenere il valore di induzione prefissato. Si tratta di risolvere il problema diretto, ad esempio col metodo delle forze magnetomotrici parziali.
Per il tronco in ghisa si ha:
![]()
Il flusso nel circuito sarà:
![]()
Per il traferro si ha:
lT = 3·10−3 [m]
ST = 1,05·S1 = 1,05·16·10−4 = 16,8·10−4 [m2]
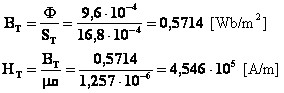
La forza magnetomotrice necessaria a sostenere il valore prefissato di induzione vale:
![]()
Passo d)
Verifichiamo se il valore di forza magnetomotrice calcolata soddisfa l’accuratezza prefissata. Essendo FMMC > 1260 [A] la condizione non è soddisfatta.
Passo e)
Scelgo un nuovo valore di induzione. Essendo il tentativo precedente fallito per eccesso del valore di FMMC, la nuova scelta dovrà essere per un valore inferiore di induzione. Scelgo il valore intermedio tra il minimo tabulato ed il valore del tentativo precedente:
![]()
passo c2)
Calcoliamo la FMMC necessaria a sostenere il valore di induzione prefissato.
Per il tronco in ghisa si ha:
![]()
ottenuto dalla lettura della tabella di magnetizzazione con relativa interpolazione lineare.
Il flusso nel circuito sarà:
![]()
Per il traferro si ha:
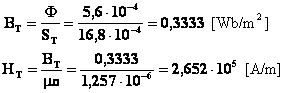
La forza magnetomotrice necessaria a sostenere il valore prefissato di induzione vale:
![]()
Passo d2)
Verifichiamo se il valore di forza magnetomotrice calcolata soddisfa l’accuratezza prefissata. Essendo FMMC > 1260 [A] la condizione non è soddisfatta.
Passo e2)
Scelgo un nuovo valore di induzione. Essendo il tentativo precedente fallito per eccesso del valore di FMMC, la nuova scelta dovrà essere per un valore inferiore di induzione. Considerando il piccolo scostamento rispetto alla fascia accettabile, scelgo il valore tabulato immediatamente minore:
![]()
passo c3)
Calcoliamo la FMMC necessaria a sostenere il valore di induzione prefissato.
Per il tronco in ghisa si ha:
![]()
ottenuto dalla lettura della tabella di magnetizzazione.
Il flusso nel circuito sarà:
![]()
Per il traferro si ha:
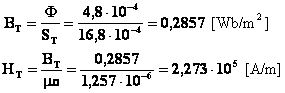
La forza magnetomotrice necessaria a sostenere il valore prefissato di induzione vale:
![]()
Passo d3)
Verifichiamo se il valore di forza magnetomotrice calcolata soddisfa l’accuratezza prefissata. Essendo:
![]()
la condizione è soddisfatta.
Passo f)
I valori di induzione e di flusso che soddisfano l’accuratezza prefissata sono quindi:
![]()
2) Determinare la corrente nell’avvolgimento affinché il flusso nel circuito magnetico sia quello sopra calcolato.
Nella precedente parte dell’esercizio abbiamo calcolato in modo approssimato quale flusso viene indotto dalla corrente di 2 [A]. Ora vogliamo vedere quale corrente è in effetti necessaria per sostenere il flusso di 4,8·10−4 [Wb]. Basterà allo scopo calcolare:
![]()
3) Determinare l’induttanza dell’avvolgimento ipotizzando che sia nullo il flusso disperso.
L’induttanza dell’avvolgimento dipende dal flusso autoconcatenato che è pari a:
![]()
Quindi l’induttanza varrà:
![]()
4) Determinare l’energia immagazzinata nel circuito magnetico.
Tale energia si può determinare in due diversi modi.
Il primo consiste nel passare attraverso l’energia specifica. In tal caso con ovvio significato dei simboli si avrà:
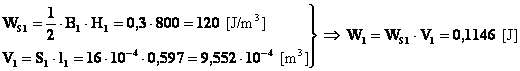
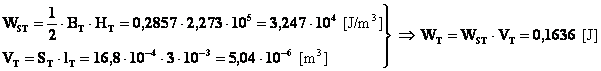
![]()
Il secondo consiste nell’utilizzare il valore dell’induttanza dell’avvolgimento:
![]()
5) Determinare la tensione magnetica tra i punti A, D.
Allo scopo possiamo usare la parte di circuito a sinistra dei punti A, D:
![]()
dove lm/2 è la lunghezza della parte in ghisa a sinistra dei punti A, D.
Ma possiamo anche usare la parte di circuito a destra dei punti A, D:
![]()
Campi e circuiti magnetici
Programma per la classe terza
Home Page