Esercizio 5 (forza portante di un elettromagnete)

Si abbia un elettromagnete a nucleo mobile (il nucleo mobile costituisce l’ancora dell’elettromagnete) realizzato in ferro fucinato con l’avvolgimento costituito da N = 1000 spire:

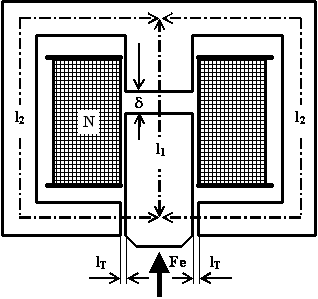
Le sue dimensioni geometriche siano le seguenti:

lunghezza media della colonna centrale comprensiva del traferro l₁ = 8 [cm];

sezione trasversale della colonna centrale A₁ = 6 [cm²];

lunghezza media dei gioghi comprensiva dei traferri l₂ = 17 [cm];

sezione trasversale dei gioghi A₂ = 3 [cm²];

lunghezza massima della corsa del nucleo mobile (ancora alla massima distanza) δ_M = 5 [mm];

lunghezza minima della corsa del nucleo mobile (ancora accostata) δ_m = 0,2 [mm];

lunghezza dei tra ferri tra nucleo mobile e gioghi l_T = 0,7 [mm].

1) Determinare il valore da assegnare alla corrente di eccitazione nell’avvolgimento affinché la forza sviluppata ad ancora accostata valga Fea = 350 [N] (si trascurino eventuali flussi dispersi e gli effetti ai bordi dei tra ferri).

La forza di attrazione che l’elettromagnete esercita sull’ancora dipende dall’induzione nel traferro e dalla superficie del polo secondo la seguente relazione:

dove Boa è il valore di induzione nel traferro tra il nucleo mobile ed il giogo quando la lunghezza del traferro ha il valore minimo (ancora accostata) pari a δ_m = 0,2 [mm].

Si può quindi calcolare il valore che deve assumere l’induzione nel traferro ad ancora accostata:

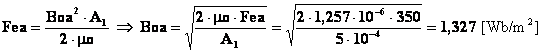
Considerando la simmetria del circuito magnetico rispetto l’asse verticale e considerando che i gioghi hanno sezione pari alla metà della sezione della colonna centrale, avremo un’induzione costante in tutto il circuito magnetico.

Per conoscere il campo magnetico nel ferro dovrò consultare le caratteristiche di magnetizzazione di questo materiale. Tali caratteristiche riportano:

Eseguendo una interpolazione lineare tra le due coppie ho:

Il campo magnetico nei traferri varrà:

Per determinare la forza magnetomotrice necessaria a sostenere questi campi conviene applicare la legge della circuitazione magnetica indifferentemente ad una delle due maglie (tra di loro uguali) del circuito magnetico.

La lunghezza complessiva della parte in ferro per ciascuna maglia è:

La lunghezza complessiva dei traferri per ciascuna maglia è:

Applicando la legge della circuitazione si trova infine la corrente di eccitazione richiesta:

2) Determinare la forza di attrazione sviluppata dall’elettromagnete quando l’ancora è alla massima distanza dall’elettromagnete e la corrente di eccitazione è quella precedentemente calcolata.

Una soluzione precisa al quesito richiede che si calcoli l’induzione nel traferro e, quindi, che si proceda per tentativi nella soluzione del problema che si presenta del tipo inverso. Tuttavia, quando si ha la massima lunghezza della corsa dell’ancora accade che nel circuito magnetico quasi tutta la tensione magnetica cade nel traferro così che si può trascurare la parte in ferro ed il problema si può risolvere con accettabile approssimazione per via diretta.

Trascurando la parte in ferro, la legge della circuitazione applicata ad una delle due maglie dice che:

dove l_Ts è la lunghezza complessiva del traferro ad ancora massimamente staccata:

Risolvendo rispetto al campo si ha:

A tale campo corrisponde l’induzione:

Si nota come l’induzione si è ridotta di circa cinque volte; praticamente l’induzione, se si trascura il ferro, risulta inversamente proporzionale alla lunghezza del traferro. Siccome poi la forza è direttamente proporzionale al quadrato dell’induzione avremo che essa sarà inversamente proporzionale al quadrato della lunghezza del traferro:

3) Determinare la corrente necessaria per produrre la forza di 350 [N] quando l’ancora è scostata alla massima distanza dall’elettromagnete.

In tal caso nel traferro servirà ancora l’induzione di 1,327 [Wb/m²] e quindi il campo di 1,057·10⁶ [A/m]. Sempre trascurando la caduta di tensione magnetica nel ferro e con ovvio significato dei passaggi si ha:

Campi e circuiti magnetici
Programma per la classe terza
Home Page

---