Negli esempi fino ad ora visti compaiono soltanto generatori di tensione. Nel caso in cui compaiano pure generatori di corrente, se ad essi è posta in parallelo una resistenza, questa può sempre essere intesa come resistenza interna del generatore e, quindi, il generatore di corrente può essere trasformato in un generatore reale di tensione. Se il generatore di corrente non ha in parallelo alcuna resistenza diventa impossibile la trasformazione e, in tal caso, nelle equazioni applicate al circuito si deve considerare nota, e pari alla corrente impressa, la corrente nel ramo ove è inserito il generatore ideale di corrente ed, eventualmente, incognita la tensione ai capi del ramo stesso.

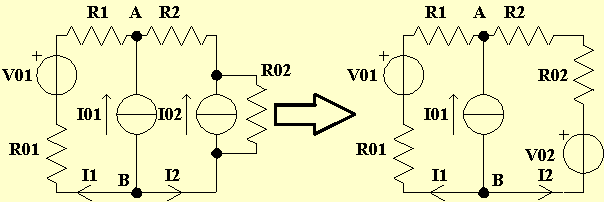
A titolo d'esempio, si determino le correnti I1 , I2 e la tensione V_AB nella rete seguente, ove V01=8 [V] , R01=0,2 [W] , R1=3,8 [W] , I01=4 [A] , I02=35 [A] , R02=0,4 [W] , R2=3,6 [W].

Per prima cosa trasformo il generatore reale di corrente in un generatore reale di tensione:

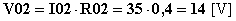
Quindi applico i principi di Kirchhoff per risolvere la rete rispetto alle incognite proposte, allo scopo applico il primo principio di Kirchhoff al nodo A ed il secondo alle due maglie contigue (adottando quale verso di maglia quello orario):

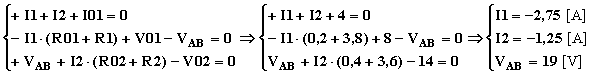
Reti elettriche in corrente continua e corrente alternata
Programma per la classe terza
Home Page